Decision Tree using CART algorithm Solved Example 1
In this tutorial, we will understand how to apply Classification And Regression Trees (CART) decision tree algorithm to construct and find the optimal decision tree for the given Play Tennis Data. Also, predict the class label for the given example…?
| Outlook | Temp | Humidity | Windy | Play |
| Sunny | Hot | High | False | No |
| Sunny | Hot | High | True | No |
| Overcast | Hot | High | False | Yes |
| Rainy | Mild | High | False | Yes |
| Rainy | Cool | Normal | False | Yes |
| Rainy | Cool | Normal | True | No |
| Overcast | Cool | Normal | True | Yes |
| Sunny | Mild | High | False | No |
| Sunny | Cool | Normal | False | Yes |
| Rainy | Mild | Normal | False | Yes |
| Sunny | Mild | Normal | True | Yes |
| Overcast | Mild | High | True | Yes |
| Overcast | Hot | Normal | False | Yes |
| Rainy | Mild | High | True | No |
| Outlook | Temp | Humidity | Windy | Play |
| Sunny | Hot | Normal | True | ? |
Solution:
First, we need to Determine the root node of the tree
In this example, there are four choices of questions based on the four variables:
Start with any variable, in this case, outlook. It can take three values: sunny, overcast, and rainy.
Start with the sunny value of outlook. There are five instances where the outlook is sunny.
In two of the five instances, the play decision was yes, and in the other three, the decision was no.
Thus, if the decision rule was that outlook: sunny → no, then three out of five decisions would be correct, while two out of five such decisions would be incorrect. There are two errors out of five. This can be recorded in Row 1.
Similarly, we will write all rules for the Outlook attribute.
Outlook
| Overcast | 4 | Yes | 4 |
| No | 0 | ||
| Sunny | 5 | Yes | 2 |
| No | 3 | ||
| Rainy | 5 | Yes | 3 |
| No | 2 |
Rules, individual error, and total for Outlook attribute
| Attribute | Rules | Error | Total Error |
| Outlook | Sunny → No | 2/5 | 4/14 |
| Overcast → Yes | 0/4 | ||
| Rainy → Yes | 2/5 |
Temp
| Hot | 4 | Yes | 2 |
| No | 2 | ||
| Mild | 6 | Yes | 4 |
| No | 2 | ||
| Cold | 4 | Yes | 3 |
| No | 1 |
Rules, individual error, and total for Temp attribute
| Attribute | Rules | Error | Total Error |
| Temp | Hot → No | 2/4 | 5/14 |
| Mild → Yes | 2/6 | ||
| Cool → Yes | 1/4 |
Humidity
| High | 7 | Yes | 3 |
| No | 4 | ||
| Normal | 7 | Yes | 6 |
| No | 1 |
Rules, individual error, and total for Humidity attribute
| Attribute | Rules | Error | Total Error |
| Humidity | High→ No | 3/7 | 4/14 |
| Normal → Yes | 1/7 |
Windy
| False | 8 | Yes | 6 |
| No | 2 | ||
| True | 6 | Yes | 3 |
| No | 3 |
Rules, individual error, and total for Humidity attribute
| Attribute | Rules | Error | Total Error |
| Windy | True → No | 3/6 | 5/14 |
| False → Yes | 2/8 |
Consolidated rules, errors for individual attributes values, and total error of the attribute are given below.
| Attribute | Rules | Error | Total Error |
| Outlook | Sunny → No | 2/5 | 4/14 |
| Overcast → Yes | 0/4 | ||
| Rainy → Yes | 2/5 | ||
| Temp | hot → No | 2/4 | 5/14 |
| Mild → Yes | 2/6 | ||
| Cool → Yes | 1/4 | ||
| Humidity | high → No | 3/7 | 4/14 |
| Normal → Yes | 1/7 | ||
| Windy | False → Yes | 2/8 | 5/14 |
| True → No | 3/6 |
From the above table, we can notice that the attributes Outlook and Humidity have the same minimum error that is 4/14. Hence we consider the individual attribute value errors. The outlook attribute has one rule which generates zero error that is the rule Overcast → Yes. Hence we consider the Outlook as the splitting attribute.
Now we build the tree with Outlook as the root node. It has three branches for each possible value of the outlook attribute. As the rule, Overcast → Yes generates zero error. When the outlook attribute value is overcast we get the result as Yes. For the remaining two attribute values we consider the subset of data and continue building the tree. Tree with Outlook as root node is,
Now, for the left and right subtrees, we write all possible rules and find the total error. Based on the total error table, we will construct the tree.
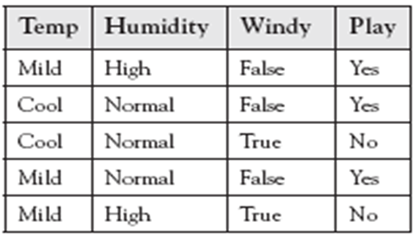
Left subtree,
Consolidated rules, errors for individual attributes values, and total error of the attribute are given below.
From the above table, we can notice that Humidity has the lowest error. Hence Humidity is considered as the splitting attribute. Also, when Humidity is High the answer is No as it produces zero errors. Similarly, when Humidity is Normal the answer is Yes, as it produces zero errors.
Right subtree,
Consolidated rules, errors for individual attributes values, and total error of the attribute are given below.
From the above table, we can notice that Windyhas the lowest error. Hence Windy is considered as the splitting attribute. Also, when Windy is False the answer is Yes as it produces zero errors. Similarly, when Windy is True the answer is No, as it produces zero errors.
The final decision tree for the given Paly Tennis data set is,
Also, from the above decision tree the prediction for the new example:
is, Yes
Summary:
In this tutorial, we understood, how to apply Classification And Regression Trees (CART) decision tree algorithm (solved example 1) to construct and find the optimal decision tree. If you like the tutorial share it with your friends. Like the Facebook page for regular updates and YouTube channel for video tutorials.