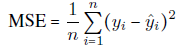The complexity of any classification or regression algorithm depends on the number of inputs to the model. This determines the time and space complexity and the necessary number of training examples to train such a classification or regression algorithm. In this article, we discuss what is dimensionality reduction, how dimensionality reduction is implemented, and the advantages of dimensionality reduction in Machine Learning.
Introduction to Dimensionality reduction in Machine Learning
In many learning problems, the datasets have a large number of variables. Sometimes, the number of variables is more than the number of observations. For example, in many scientific fields such as image processing, mass spectrometry, time series analysis, internet search engines, and automatic text analysis the number of input variables is more than the number of inputs. Statistical and machine learning methods have difficulty in dealing with such high-dimensional data. Normally the number of input variables is reduced before applying the machine learning algorithm.
In statistical and machine learning, dimensionality reduction or dimension reduction is the process of reducing the number of variables under consideration by obtaining a smaller set of principal variables.
Dimensionality reduction may be implemented in two ways.
1. Feature selection: In feature selection, we are interested in finding k of the total of n features that give us the most information and we discard the other (n−k) dimensions. We are going to discuss subset selection as a feature selection method.
2. Feature extraction: In feature extraction, we are interested in finding a new set of k features that are the combination of the original n features. These methods may be supervised or unsupervised depending on whether or not they use the output information. The best known and most widely used feature extraction methods are Principal Components Analysis (PCA) and Linear Discriminant Analysis (LDA), which are both linear projection methods, unsupervised and supervised respectively.
Measures of error
In both methods, we require a measure of the error in the model.
1. In regression problems, we may use the Mean Squared Error (MSE) or the Root Mean Squared Error (RMSE) as the measure of error. MSE is the sum, over all the data points, of the square of the difference between the predicted and actual target variables, divided by the number of data points.
Here,
are the observed values and
are the predicted values.
2. In classification problems, we may use the misclassification rate as a measure of the error. This is defined as follows:
Advantages of dimensionality reduction in Machine Learning
There are several reasons why we are interested in reducing dimensionality.
- In most learning algorithms, the complexity depends on the number of input dimensions, d, as well as on the size of the data sample, N, and for reduced memory and computation, we are interested in reducing the dimensionality of the problem. Decreasing d also decreases the
- The complexity of the inference algorithm during testing.
- When an input is decided to be unnecessary, we save the cost of extracting it.
- Simpler models are more robust on small datasets. Simpler models have less variance, that is, they vary less depending on the particulars of a sample, including noise, outliers, and so forth.
- When data can be explained with fewer features, we get a better idea about the process that underlies the data, which allows knowledge extraction.
- When data can be represented in a few dimensions without loss of information, it can be plotted and analyzed visually for structure and outliers.
Feature (Subset) Selection in Machine Learning
In machine learning subset selection, sometimes also called feature selection or variable selection, or attribute selection is the process of selecting a subset of relevant features (variables, predictors) for use in model construction.
Feature selection techniques are used for four reasons:
- simplification of models to make them easier to interpret by researchers/users
- shorter training times,
- to avoid the curse of dimensionality
- enhanced generalization by reducing overfitting
The central premise when using a feature selection technique is that the data contains many features that are either redundant or irrelevant and can thus be removed without incurring much loss of information. There are several approaches to subset selection. In these notes, we discuss two of the simplest approaches known as forward selection and backward selection methods.
Forward selection
In forward selection, we start with no variables and add them one by one, at each step adding the one that decreases the error the most, until any further addition does not decrease the error (or decreases it only sightly).
Forward Selection Procedure

Remarks
- In this procedure, we stop if adding any feature does not decrease the error E. We may even decide to stop earlier if the decrease in error is too small, where there is a user-defined threshold that depends on the application constraints.
- This process may be costly because to decrease the dimensions from n to k, we need to train and test the system
times.
Backward selection
In sequential backward selection, we start with the set containing all features and at each step remove the one feature that causes the least error.
Backward Selection Procedure
Summary: Dimensionality reduction in Machine Learning
This article discusses what is dimensionality reduction, how dimensionality reduction is implemented, and the advantages of dimensionality reduction in Machine Learning. If you like the material share it with your friends. Like the Facebook page for regular updates and the YouTube channel for video tutorials.